What is Edmonds-Karp Algorithm? | Edmonds-Karp Algorithm

INTRODUCTION

Edmonds-Karp algorithm is an implementation of the Ford–Fulkerson method for computing the maximum flow in a given flow network with the time complexity of O(V x E^2), where V is the number of vertices and E is the number of edges. What is Ford-Fulkerson method? It is a "greedy" method based on the idea of finding paths (it is called an "augmenting path" in network flow) from the source (start node) to the sink (end node), through which we can send the flow given available capacity and current amount of flow in each edge, until we run out of them.

ABOUT FLOW NETWORK

Flow network is a directed graph with vertices and edges having its own flow and capacity. Flow is the amount of flow that passes through the edge and the capacity is the amount of flow that the edge can hold. There must exist the source (start node) and the sink (end node) of the flow in the network. In flow network problems, the goal is to get the maximum flow of each edge given its capacity in order to obtain the maximum flow from the source to the sink of the network.

INVARIANTS

Here is a list of invariants of the flow network:

The total amount of flow going into a node must equal to the total amount of flow going out from a node. For the source and sink, the amount of flow going out from the source must equal to the amount of flow going into the sink.
The flow must never exceed the capacity of an edge. In other words, Capacity(u, v) - Flow(u, v) >= 0
If there exists an edge between two vertices, then there can exist a virtual edge flowing in opposite direction with the same amount of negative flow. In other words, Flow(u, v) = -Flow(v, u)

THE ALGORITHM

*Each edge of the initial setup of the graph starts with the zero flow.

Use Breadth First Search to find a possible path P from the source to the sink, such that all of the edges in P have available capacity.
If found in step 1), fill each edge's flow that is equivalent to the minimum capacity of the edges in the path.
For each "actual" edge in the augmenting path, add the flow. For each reverse "virtual" edge in the path, subtract the flow.
Repeat from 1) to 3) until no more augmenting path exists.

PERFORMANCE OF THE EDMONDS-KARP

Claim : Given a flow network with n vertices and m edges, the E-K algorithm computes a maximum flow in O(n*(m^2)) time.

Proof :

Lemma 1. The shortest path between the source and all other vertices is always increasing (monotonic) in the residual graph.

- (Proof by Contradiction)

Assume the shortest path from the source to all other vertices can decrease after an augmentation.

Let df(s, v) = shortest path from s to v before augmentation and df'(s, v) = shortest path from s to v after augmentation

then, df'(s,v) < df(s, v)

Also, assume there exists some vertex u that exists in the shortest path from s to v, and s to v is 1 more than the shortest path from s to u. (In other words, df'(s, u) = df'(s, v) - 1 )

Here, the shortest path from s to u did not decrease with the new flow f', since we chose the shortest path from s to v to be decreasing after the new flow f'. So, df'(s, u) >= df(s, u)

If the edge between u and v remained in the residual graph after flow augmentations, the following relationships would exist:

1) df(s, v) <= df(s, u) + 1 (triangular inequality)

2) df(s, v) <= df'(s,u) + 1 (shortest path decreases with the new flow)

3) df(s, v) <= df'(s, v) (the relationship between (s,u) and (s,v))

Since 3) contradicts the assumption we made above, which is df'(s, v) < df(s, v), the proof shows that the shortest path increases monotonically in the residual graph, resulting the length of the iteration of the algorithm to O(m = number of edges).

Lemma 2. The number of flow augmentations is no more than n vertices * m edges.

Proof:

Let u and v represent any vertices that are connected by an edge and s be the source. When that edge becomes critical,

Df (s, v) = Df (s, u) + 1. (Df represents the distance between two vertices during the flow of f)

If this flow gets augmented, the edge (u, v) disappears as the flow of the edge reaches its capacity. The edge can reappear when

the flow in this edge decreases as its reverse counterpart appears. Let f' is this new happening flow. Then,

Df' (s, u) = Df'(s, v) + 1

Because the shortest path increases as in the first lemma,

Df' (s, u) = Df'(s, v) + 1

Df' (s, u) >= Df(s, v) + 1

Df' (s, u) >= Df(s, u) + 2

The intermediate vertices on the shortest path from s to u cannot contain vertices s, u, or t. Therefore, the distance to vertex u is at most |n|−2 . Since the distance from the source increases by at least 2 every time an edge becomes critical, the edge (u,v) can become critical at most |n|−2 times. An edge can become critical at most O(|n|) times. Now, there are a total of O(|m|) edges.

Hence, the overall number of augmentations is no more than n * m iterations.

PERFORMANCE OF THE EDMONDS-KARP

Claim : Given a flow network with n vertices and m edges, the E-K algorithm computes a maximum flow in O(n*(m^2)) time.

Proof :

Lemma 1. The shortest path between the source and all other vertices is always increasing (monotonic) in the residual graph.

- (Proof by Contradiction)

Assume the shortest path from the source to all other vertices can decrease after an augmentation.

Let df(s, v) = shortest path from s to v before augmentation and df'(s, v) = shortest path from s to v after augmentation

then, df'(s,v) < df(s, v)

Also, assume there exists some vertex u that exists in the shortest path from s to v, and s to v is 1 more than the shortest path from s to u. (In other words, df'(s, u) = df'(s, v) - 1 )

Here, the shortest path from s to u did not decrease with the new flow f', since we chose the shortest path from s to v to be decreasing after the new flow f'. So, df'(s, u) >= df(s, u)

If the edge between u and v remained in the residual graph after flow augmentations, the following relationships would exist:

1) df(s, v) <= df(s, u) + 1 (triangular inequality)

2) df(s, v) <= df'(s,u) + 1 (shortest path decreases with the new flow)

3) df(s, v) <= df'(s, v) (the relationship between (s,u) and (s,v))

Lemma 2. The number of flow augmentations is no more than n vertices * m edges.

Proof:

Let u and v represent any vertices that are connected by an edge and s be the source. When that edge becomes critical,

Df (s, v) = Df (s, u) + 1. (Df represents the distance between two vertices during the flow of f)

If this flow gets augmented, the edge (u, v) disappears as the flow of the edge reaches its capacity. The edge can reappear when

the flow in this edge decreases as its reverse counterpart appears. Let f' is this new happening flow. Then,

Df' (s, u) = Df'(s, v) + 1

Because the shortest path increases as in the first lemma,

Df' (s, u) = Df'(s, v) + 1

Df' (s, u) >= Df(s, v) + 1

Df' (s, u) >= Df(s, u) + 2

Hence, the overall number of augmentations is no more than n * m iterations.

MIN-CUT MAX FLOW THEOREM

In flow network, the theorem states that the maximum amount of flow passing from the source to the sink is equal to the total capacities of the edges in the minimum cut, a subset of edges which can separate the subset of vertices including the source from the subset of vertices including the sink if removed.

Claim: F* = C(S, T)*

max flow min capacities of the edges in the cut from S to T

Proof:

Lemma 1. Any flow of the network cannot exceed C(S, T), the total capacities of the edges from the source to the sink.

Corollary. F* <= C(S, T)*

First, starting with the zero flow, we find an augmenting path from S to T.

Among all the edges in the augmenting path, we add the flow that equals to the minimum capacity of the edge in the path into each edge and subtract the same amount of flow from its reverse counterpart. This is the process of making our residual graph of the flow network that reflects by how much each edge can afford more flow passing through. We repeat finding augmenting paths until we cannot find any path from S to T that can afford more flow.

When we come across this situation, we can divide the vertices into two groups given each residual flow in each edge: the group V where all the vertices can be reached from the source, and the group V^c where all the vertices cannot be reached from the source. Consider a pair of vertices, u and v, where u is any vertex in group V and v is any vertex in group V^c.

Then,

flow(u, v) = capacity(u, v): The flow (u,v) must have been maximized otherwise there would still exist an augmenting path. Therefore,
flow(V, V^c) = capacity(V, V^c) Finally, by our corollary,
F* = C(S, T)*

INTRODUCTION

The Edmonds-Karp algorithm is an implementation of the Ford–Fulkerson method for computing the maximum flow in a given flow network with the time complexity of O( ), where V is the number of vertices and E is the number of edges. What is the Ford-Fulkerson method? It is a "greedy" method based on the idea of finding paths (called "augmenting paths" in network flow) from the source (start node) to the sink (end node), through which we can send the flow given available capacity and current amount of flow in each edge, until we run out of them.

ABOUT FLOW NETWORK

A flow network is a directed graph with vertices and edges having its own flow and capacity. Capacity is the amount of flow that the edge can hold. There must exist the source (start node) and the sink (end node) of the flow in the network. In flow network problems, the goal is to obtain the maximum flow from the source to the sink. For this reason, we build a residual graph, which shows the residual capacity, the difference between the current flow and capacity in each forward edge. In the picture below, the right is the residual graph for the network on the left. Notice that the blue edges in the residual graph represent the backward edges of which the capacity equals 0 and the flow equals the negative flow of the forward edge. Also notice that the forward edge in the residual graph disappears when the flow in its corresponding edge in the original graph equals the capacity.

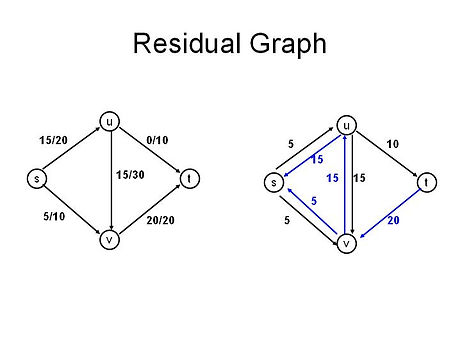
INVARIANTS

Here is a list of invariants of the flow network:

The total amount of flow going into a node must equal the total amount of flow going out from a node. For the source and sink, the amount of flow going out from the source must equal the amount of flow going into the sink.
The flow must never exceed the capacity of an edge. In other words, Capacity(u, v) - Flow(u, v) >= 0
If there exists an edge between two vertices, then there can exist a virtual edge flowing in opposite direction with the same amount of negative flow. In other words, Flow(u, v) = -Flow(v, u)

THE ALGORITHM

*Each edge of the initial setup of the graph starts with the zero flow.

*Assume the current graph have the flows as shown after following the steps several times:

In the residual graph for the network graph above, Use Breadth First Search to find a possible path P from the source to the sink.

2. If found, update the residual graph by adding the flow that equals

the minimum current residual capacity on the path into each

backward edge that leads from t to s. Also, do not forget to

subtract the same amount from each forward edge

in augmenting path. Update the network graph in accordance with

the update in residual graph.

Residual

Network

3. Repeat 1. and 2. until no more augmenting paths from s to t exist.

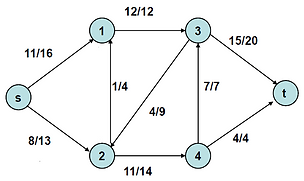
Pseudocode

PERFORMANCE OF EDMONDS-KARP

Claim : Given a flow network with V vertices and E edges, the E-K algorithm computes a maximum flow in O( ) time.

Proof :

Lemma 1. The minimum length (number of edges) of an augmenting path from the source to any vertex v is non-decreasing (monotonic) in

the residual graph. In other words, let g be the flow obtained from flow f with an augmentation along a path p of minimum length.

Then, for each vertex v,

- (Proof by Contradiction)

Assume the shortest path from the source to all other vertices can decrease after an augmentation.

Let df(s, v) = shortest path from s to v before augmentation and df'(s, v) = shortest path from s to v after augmentation

then, df'(s,v) < df(s, v)

Also, assume there exists some vertex u in the shortest path from s to v, and s to v is 1 more than the shortest path from s to u. (In other words, df'(s, u) = df'(s, v) - 1 )

Here, the shortest path from s to u did not decrease with the new flow f', since we chose the shortest path from s to v to be decreasing after the new flow f'. So, df'(s, u) >= df(s, u)

If the edge between u and v remained in the residual graph after flow augmentations, the following relationships would exist:

1) df(s, v) <= df(s, u) + 1 (triangular inequality)

2) df(s, v) <= df'(s,u) + 1 (shortest path decreases with the new flow)

3) df(s, v) <= df'(s, v) (the relationship between (s,u) and (s,v))

Since 3) contradicts the assumption we made above, which is df'(s, v) < df(s, v), the proof shows that the shortest path is non-decreasing in the residual graph, implying that the number of iterations of the algorithm is O(E).

Lemma 2. The number of flow augmentations is O(V x E) .

Proof:

Let u and v represent any vertices that are connected by an edge and s be the source. When that edge becomes critical,

Df (s, v) = Df (s, u) + 1. (Df represents the distance between two vertices during the flow of f)

If this flow gets augmented, the edge (u, v) disappears as the flow of the edge reaches its capacity. The edge can reappear when

the flow in this edge decreases as its reverse counterpart appears.

Let f' is this new happening flow. Then,

Df' (s, u) = Df'(s, v) + 1

Because the shortest path increases as in the first lemma,

Df' (s, u) = Df'(s, v) + 1

Df' (s, u) >= Df(s, v) + 1

Df' (s, u) >= Df(s, u) + 2

The intermediate vertices on the shortest path from s to u cannot contain vertices s, u, or t. Therefore, the distance to vertex u is at most V−2 . Since the distance from the source increases by at least 2 every time an edge becomes critical, the edge (u,v) can become critical at most V−2 times. An edge can become critical at most O(V) times. Now, there are a total of O(E) edges.

Hence, the overall number of iterations is no more than V x E.

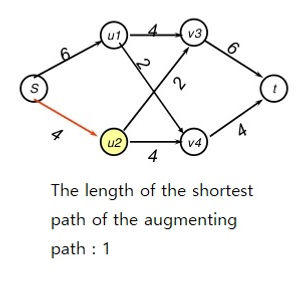
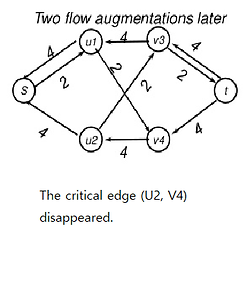
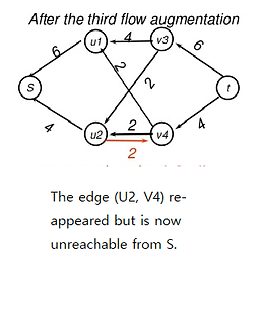
MIN-CUT MAX FLOW THEOREM

In a flow network, this theorem states that the maximum amount of flow passing from the source to the sink is equal to the total capacities of the edges in the minimum cut, a subset of edges which can separate the subset of vertices including the source from the subset of vertices including the sink if removed.

Claim: F* = C(S, T)*

max flow min capacities of the edges in the cut from S to T

Proof:

Lemma 1. Any flow of the network cannot exceed C(S, T), the total capacities of the edges from the source to the sink.

Corollary. F* <= C(S, T)*

First, starting with zero flow, we find an augmenting path from S to T.

Among all the edges in the augmenting path, we add the flow that equals the minimum capacity in the path into each edge and subtract the same amount of flow from its reverse counterpart. This is the process of making our residual graph of the flow network that reflects by how much each edge can afford more flow passing through. We repeat finding augmenting paths until we cannot find any path from S to T that can afford more flow.

When we come across this situation, we can divide the vertices into two groups given each residual flow in each edge: the group V where all the vertices can be reached from the source, and the group where all the vertices cannot be reached from the source. Consider a pair of vertices, u and v, where u is any vertex in group V and v is any vertex in group .

Then,

flow(u, v) = capacity(u, v): The flow (u,v) must have been maximized otherwise there would still exist an augmenting path. Therefore,
flow(V, ) = capacity(V, ) Finally, by our corollary,
F* = C(S, T)*

EDMONDS-KARP ALGORITHM

INTRODUCTION

ABOUT FLOW NETWORK

INVARIANTS

THE ALGORITHM

PERFORMANCE OF THE EDMONDS-KARP

PERFORMANCE OF THE EDMONDS-KARP

MIN-CUT MAX FLOW THEOREM

INTRODUCTION

ABOUT FLOW NETWORK

INVARIANTS

THE ALGORITHM

Pseudocode

PERFORMANCE OF EDMONDS-KARP

MIN-CUT MAX FLOW THEOREM